Преобразования y = sin x
Рассмотрим примеры решения заданий с преобразованиями y=sinx.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание
Пример 4
Построить график y=-3sin12x-32-2 с помощью преобразований функции y=sinx.
Решение
Необходимо привести функцию к виду ±k1·f±k2·x+a+b. Для этого:
y=-3sin12x-32-2=-3sin12(x-3)-2
Видно, что k1=3, k2=12, a=-3, b=-2. Так как перед k1 имеется -, а перед k2 — нет, тогда получим цепочку преобразований вида:
y=sin(x)→y=3sin(x)→y=3sin12x→y=-3sin12x→→y=-3sin12x-3→y=-3sin12(x-3)-2
Подробное преобразование синусоиды. При построении графика исходной синусоиды y=sin(x) получаем, что наименьшим положительным периодом считается T=2π. Нахождение максимума в точках π2+2π·k; 1, а минимума — -π2+2π·k; -1, k∈Z.
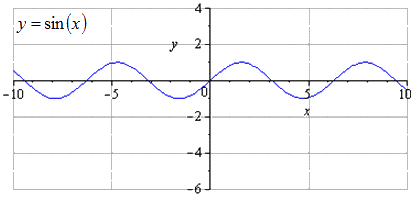
Производится растягивание по Оу втрое, значит возрастание амплитуды колебаний возрастет в 3 раза. T=2π — это наименьший положительный период. Максимумы переходят в π2+2π·k; 3, k∈Z , минимумы — -π2+2π·k; -3, k∈Z.
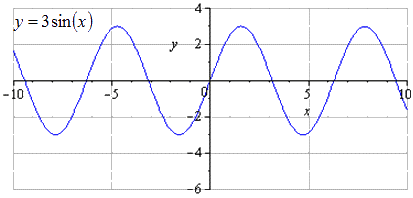
При растягивании по Ох вдвое получаем, что наименьший положительный период увеличивается в 2 раза и равняется T=2πk2=4π. Максимумы переходят в π+4π·k; 3, k∈Z, минимумы – в -π+4π·k; -3, k∈Z.
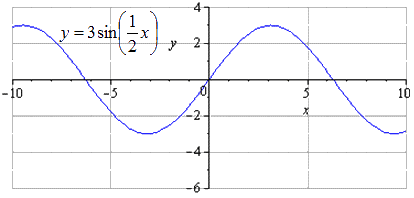
Изображение производится симметрично относительно Ох. Наименьший положительный период в данном случае не меняется и равняется T=2πk2=4π. Переход максимума выглядит как -π+4π·k; 3, k∈Z, а минимума – π+4π·k; -3, k∈Z.
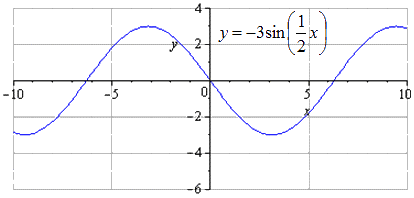
Производится сдвижение графика вниз на 2 единицы. Изменение наименьшего общего периода не происходит. Нахождение максимумов с перехождением в точки -π+3+4π·k; 1, k∈Z, минимумов — π+3+4π·k; -5, k∈Z.
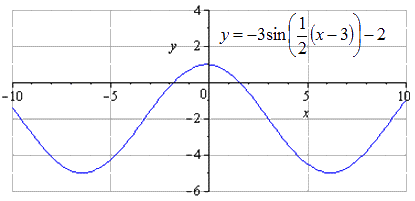
На данном этапе график тригонометрической функции считается преобразованным.
Показательная функция
Преобразования показательной функции рассмотрим на примерах.
Пример 2
Произвести построение графика показательной функции y=-1212(2-x)+8.
Решение.
Преобразуем функцию, исходя из свойств степенной функции. Тогда получим, что
y=-1212(2-x)+8=-12-12x+1+8=-12·12-12x+8
Отсюда видно, что получим цепочку преобразований y=12x:
y=12x→y=12·12x→y=12·1212x→→y=-12·1212x→y=-12·12-12x→→y=-12·12-12x+8
Получаем, что исходная показательная функция имеет вид
Сжимание вдвое вдоль Оу дает
Растягивание вдоль Ох
Симметричное отображение относительно Ох
Отображение симметрично относительно Оу
Сдвигание на 8 единиц вверх
Просмотр данных в цифровом виде
Чтобы просмотреть
значения точки на графике в цифровом виде проделайте следующее:
1. нажмите и
удерживайте левую кнопку мыши в рабочем поле графика. Курсор мыши примет
крестообразную форму;
2. установите
курсор мыши на интересующую Вас точку на графике. В заголовке графика Вы
увидите дату и время интервала агрегации, значение на шкале цен, на которое в
данный момент показывает указатель (Y), цену открытия периода (O), максимальную за период цену сделок (H), минимальную за период цену сделок (L), цену закрытия периода (С).
При
позиционировании курсора на экране вне графика в его заголовок выводится
надпись «Вне диапазона».
Японские свечи
Этот метод отображения цены придуман в Японии, в 17 веке торговцами на бирже риса, и с тех пор получил широкую известность во всем мире. График в виде японских свечей, пожалуй, наиболее популярный, информативный и удобный для торговли. Выглядит он следующим образом:
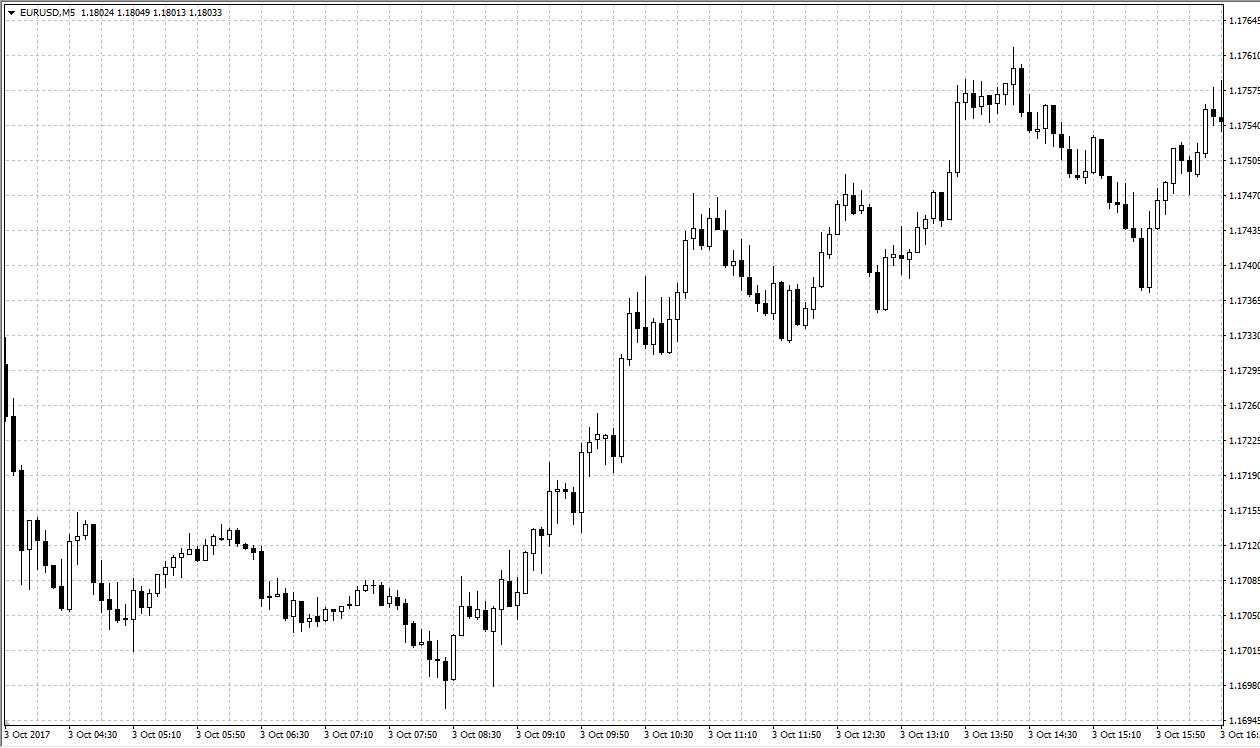Отображение графика цены в виде японских свечей
Благодаря каждой свече можно узнать такие параметры цены как:
- цена открытия
- цена закрытия
- минимальная цена за единицу времени
- максимальная цена за единицу времени
Давайте подробнее разберем, как читать график японских свечей, чтобы понимать, как обстоят дела на бирже.
Каждая свеча представляет собой колебание цены за один временной период, который выбирает трейдер. Т.е. одна свеча, например, может отображать все движения цены в течение 5 минут, часа, дня и т.д.
Как проходит один период, например час, так начинает формироваться следующая свеча, время формирования которой займет тоже один час. Временной период (таймфрейм) устанавливается трейдером в настройках биржевого терминала.
Схематичное представление японских свечей
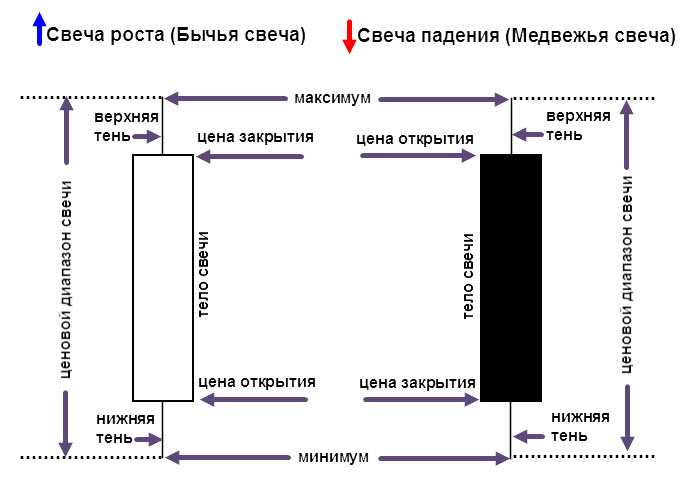Японские свечи
Все параметры свечей имеют свои общепринятые обозначения на английском языке.
- Открытие — Open (O)
- Закрытие — Close (C)
- Максимум — High (H)
- Минимум — Low (L)
Белая свеча обозначает рост за определенный промежуток времени, а черная — падение. Цвета свечей можно установить на свое усмотрение в настройках терминала.
Данные OHLC свечи отображаются, если навести на нее курсор мыши. Вот как эти параметры отображаются в самом популярном терминале MetaTrader
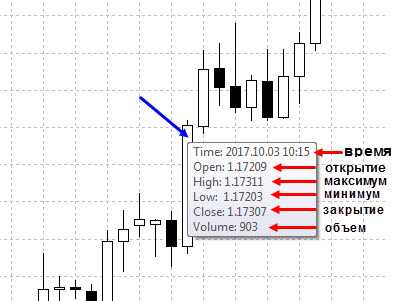Числовые данные свечи
Т.к. колебания цен хаотичны, то и свечи бывают абсолютно разных видов. Например, свечи могут быть без теней, или когда максимумом является цена открытия, а минимумом цена закрытия. Либо цена открытия и закрытия могут быть равны, и т.д.
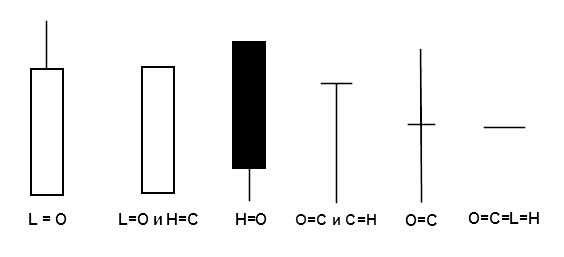Примеры некоторых видов свечей
По свече можно понять, как проходили торги в данный отрезок времени, и кто, в конце концов, взял превосходство продавцы или покупатели. Так же, хорошо видно настроение участников рынка: насколько широкий диапазон у свечи, и как игроки осторожничают, когда диапазон мал. Это хорошо видно перед выходом каких-нибудь важных новостей, когда рынок замирает в ожидании, рисуя свечи с маленьким диапазонам. Трейдеры еще говорят про такой рынок, что он стоит на месте.
Продемонстрируем вам отличный пример, когда благодаря свечам, хорошо видна активность и реакция на новости:
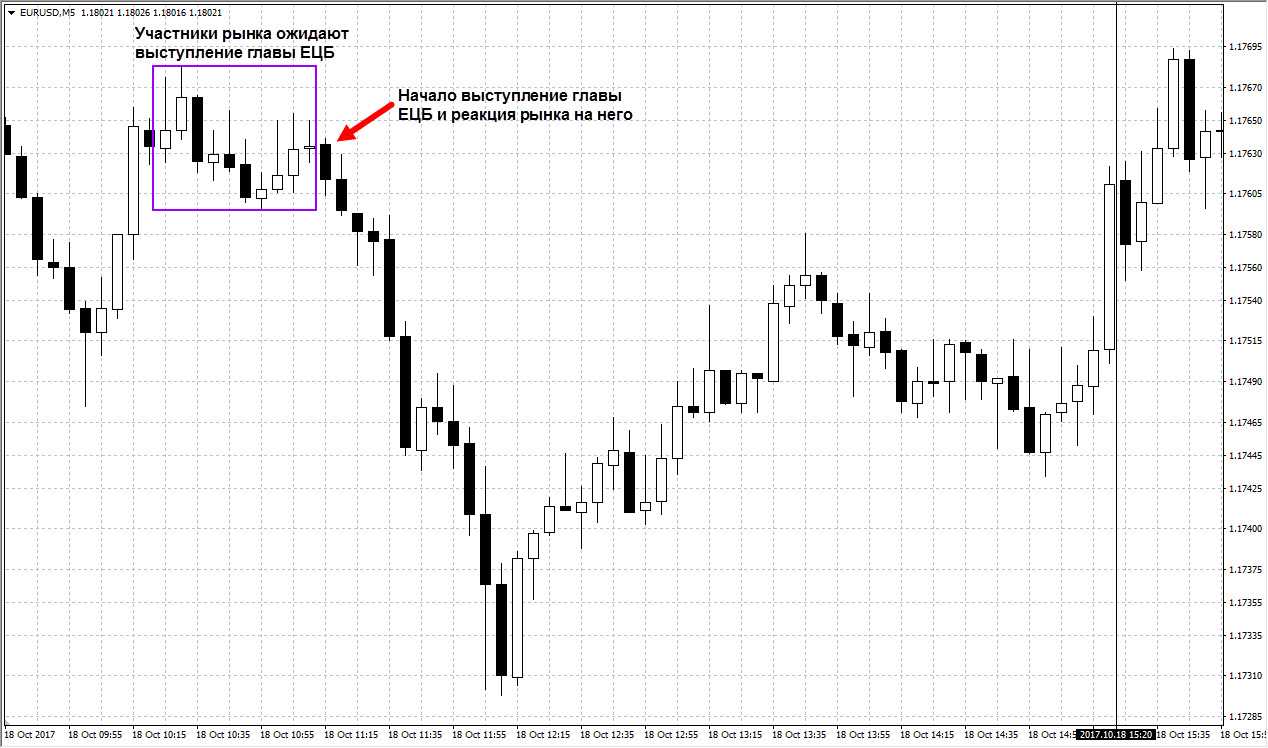Реакция рынка на новости
На ожидании выступления главы ЕЦБ цена двигалась в небольшом коридоре. С началом выступления активность резко возросла и цена упала. Такое случается сплошь и рядом на выходе новостей и рыночной статистики. Поэтому, в такие моменты надо быть предельно осторожным.
| Научитесь торговать. Пройдите индивидуальное обучение трейдингу. |
Достаточно часто, благодаря графику японских свечей, можно заранее обнаружить развороты на бирже.
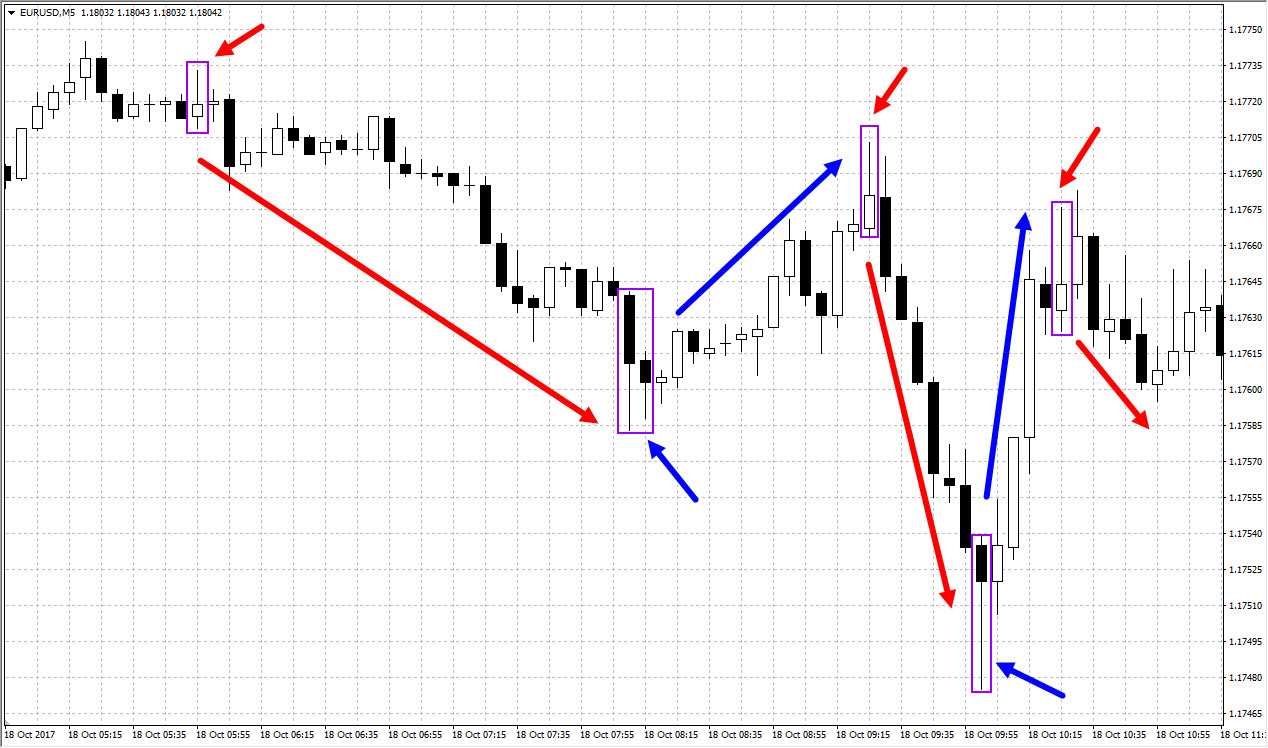Точки разворота цены
Обратите внимание, какие длинные тени у свечей по отношению к телу. Это часто является предвестником движения цены в обратную сторону
Существуют различные комбинаций, состоящие из одной или даже нескольких свечей, с помощью которых можно спрогнозировать разворот рынка или усиление предыдущей тенденции.
Мы рекомендуем вам в торговле использовать график в виде японских свечей. Он очень информативен и помогает читать настроение биржи.
Степенная функция
Рассмотрим решения на примерах, начиная со степенной функции.
Пример 1
Преобразовать y=x23 и построить график функции y=-12·8x-423+3.
Решение
Представим функции таким образом:
y=-12·8x-423+3=-12·8x-1223+3=-2x-1223+3
Где k1=2, стоит обратить внимание на наличие -, а=-12 , b=3. Отсюда получаем, что геометрические преобразования производятся с растяжения вдоль Оу вдвое, отображается симметрично относительно Ох, сдвигается вправо на 12 и вверх на 3 единицы
Если изобразить исходную степенную функцию, получим, что
при растягивании вдвое вдоль Оу имеем, что
Отображение, симметричное относительно Ох, имеет вид
а движение вправо на 12
движение на 3 единицы вверх имеет вид
Как создать диаграмму из нескольких листов Excel
Предположим, что на нескольких листах Excel содержатся данные о доходе за несколько лет, и требуется построить диаграмму по этим данным, чтобы показать общую тенденцию.
1. Создайте диаграмму по данным первого листа
Откройте первый рабочий лист Excel, выделите данные, которые нужно отобразить на диаграмме, откройте вкладку Вставка (Insert) и в разделе Диаграммы (Charts) выберите нужный тип диаграммы. Для нашего примера мы выберем Объёмная гистограмма с накоплением (Stack Column).
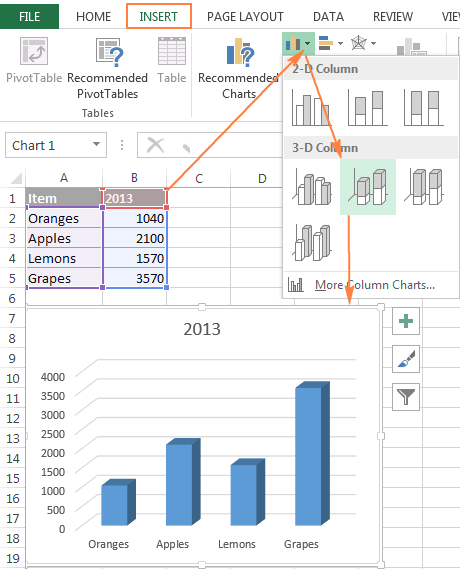
2. Добавьте второй ряд данных с другого листа
Кликните по только что созданной диаграмме, чтобы на Ленте меню появилась группа вкладок Работа с диаграммами (Chart Tools), откройте вкладку Конструктор (Design) и нажмите кнопку Выбрать данные (Select Data). Или нажмите по иконке Фильтры диаграммы (Chart Filters) справа от диаграммы и в самом низу появившегося меню, кликните ссылку Выбрать данные (Select Data).
В диалоговом окне Выбор источника данных (Select Data Source) нажмите кнопку Добавить (Add).
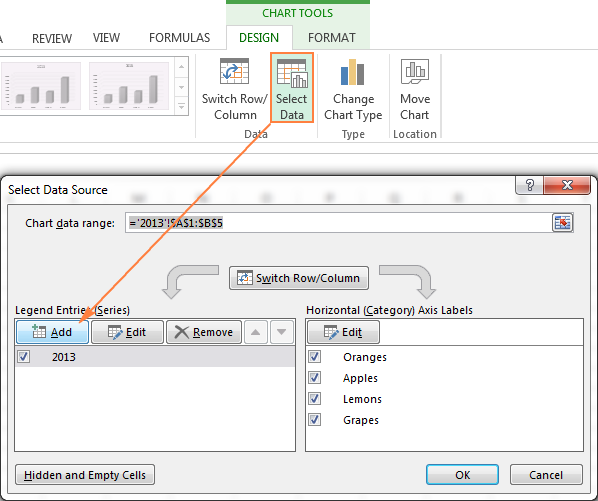
Теперь добавим второй ряд данных с другого рабочего листа. Этот момент очень важен, поэтому внимательно следуйте инструкциям. После нажатия кнопки Добавить (Add) откроется диалоговое окно Изменение ряда (Edit Series), здесь нужно нажать иконку выбора диапазона рядом с полем Значения (Series values).
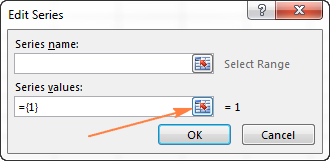
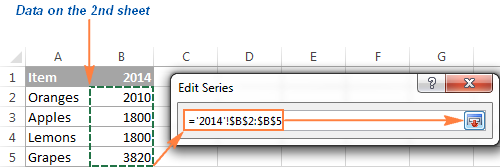
Диалоговое окно Изменение ряда (Edit Series) свернётся. Кликните по ярлычку листа, содержащего следующую часть данных, которые нужно показать на диаграмме Excel. При переключении на другой лист диалоговое окно Изменение ряда (Edit Series) останется на экране.
На втором листе выделите столбец или строку данных, которые нужно добавить на диаграмму Excel, и снова кликните по иконке выбора диапазона, чтобы диалоговое окно Изменение ряда (Edit Series) вернулось к первоначальному размеру.
Теперь кликните по иконке выбора диапазона рядом с полем Имя ряда (Series name) и выберите ячейку, содержащую текст, который нужно использовать в качестве имени ряда данных. Вновь кликните по иконке выбора диапазона, чтобы вернуться к первоначальному диалоговому окну Изменение ряда (Edit Series).
Проверьте ссылки, которые теперь появились в полях Имя ряда (Series name) и Значения (Series values), и нажмите ОК.
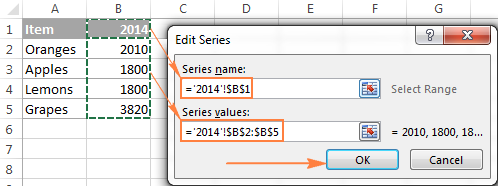
Как видно на рисунке выше, мы связали имя ряда с ячейкой B1, в которой содержится заголовок столбца. Вместо ссылки на заголовок столбца, можно ввести имя в виде текстовой строки, заключённой в кавычки, например:
Имена рядов данных появятся в легенде диаграммы, поэтому лучше придумать осмысленные и содержательные имена. На данном этапе результат должен быть примерно таким:
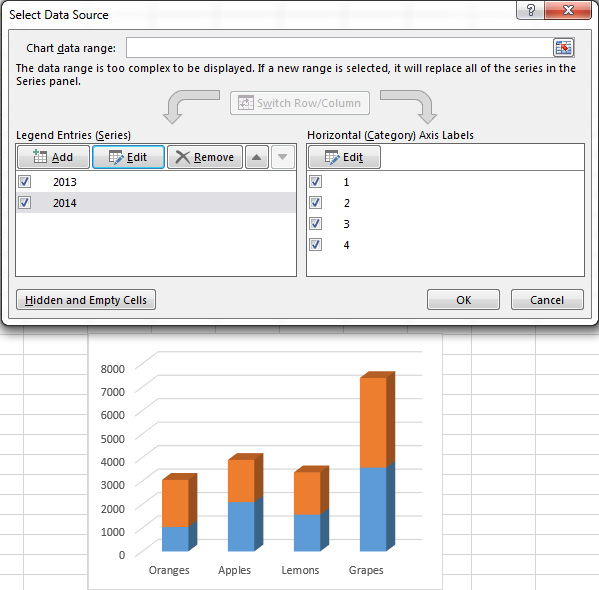
3. Добавьте еще больше рядов данных (по желанию)
Если в диаграмме должны быть показаны данные более, чем с двух рабочих листов, то повторите предыдущий этап для каждого ряда данных, который нужно добавить на диаграмму. Когда закончите, нажмите ОК в диалоговом окне Выбор источника данных (Select Data Source).
Я для примера добавил третий ряд данных, и моя диаграмма теперь выглядит так:
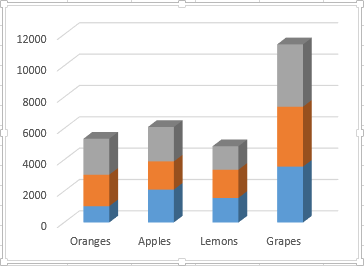
4. Настройте и улучшите диаграмму (по желанию)
При создании диаграмм в Excel 2013 и 2016 обычно автоматически добавляются такие элементы, как название диаграммы и легенда. К нашей диаграмме, составленной из содержимого нескольких листов, название и легенда не были добавлены автоматически, но мы быстро исправим это.
Выделите диаграмму, нажмите иконку Элементы диаграммы (Chart Elements) в виде зелёного креста возле правого верхнего угла диаграммы, и отметьте галочкой нужные параметры:
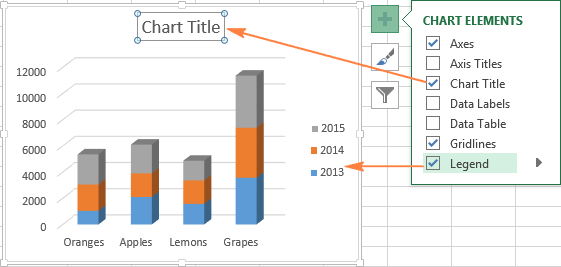
О том, как настраивать другие параметры диаграммы, такие как или , подробно рассказано в отдельной статье о настройке диаграмм Excel.
Создание диаграммы из итоговой таблицы
Решение, показанное выше, удобно только в том случае, если данные, которые нужно отобразить на диаграмме, на всех рабочих листах выстроены в одинаковом порядке, т.е. в первой строке – Oranges, во второй – Apples и т.д. В противном случае графики превратятся в нечто неразборчивое.
В данном примере расположение данных одинаково на всех трёх листах. Если требуется построить график из гораздо больших таблиц, и нет уверенности в том, что структура данных в этих таблицах одинакова, то разумнее будет сначала создать итоговую таблицу, а уже из получившейся итоговой таблицы создавать диаграмму. Чтобы заполнить итоговую таблицу нужными данными, можно использовать функцию ВПР (VLOOKUP).
Например, если рабочие листы, о которых идёт речь в этом примере, содержат данные в разном порядке, то мы можем сделать из них итоговую таблицу при помощи вот такой формулы:
И получить вот такой результат:
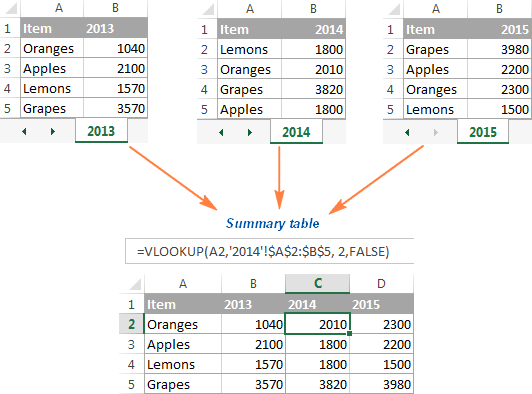
Далее просто выбираем итоговую таблицу, открываем вкладку Вставка (Insert) и в разделе Диаграммы (Charts) выбираем нужный тип диаграммы.
Тригонометрическая функция вида y=arccosx
Рассмотрим на примере тригонометрической функции вида y=arccosx.
Пример 7
Построить график функции y=2arcsin13(x-1) при помощи преобразования y=arccosx.
Решение
Для начала необходимо перейти от арккосинуса к арксинусу при помощи обратных тригонометрических функций arcsin x+arcocos x=π2. Значит, получим, что arcsinx=π2-arccosx.
Видно, что y=arccosx→y=-arccosx→y=-arccosx+π2.
Поэтапное преобразование арккосинуса и графическое изображение.
График, данный по условию
Производим отображение относительно Ох
Производим движение вверх на π2.
Таким образом, осуществляется переход от арккосинуса к косинусу. Необходимо произвести геометрические преобразования арксинуса и его графика.
Видно, что k1=2, k2=13, a=-1, b=, где отсутствует знак — у k1 и k2.
Отсюда получаем, что преобразования y=arcsinx примет вид:
y=arcsin(x)→y=2arcsin(x)→→y=2arcsin13x→y=2arcsin13(x-1)
Поэтапное преобразование графика арксинуса и графическое изображение.
График y=arcsinx имеет область определения вида x∈-1; 1, тогда интервал y∈-π2; π2 относится к области значений.
Необходимо растянуть вдвое по Оу, причем область определения останется неизменной x∈-1; 1, а область значений y∈-π; π.
Растягивание по Ох строе. Происходит расширение области определения x∈-3; 3, но область значений остается неизменной y∈-π; π.
Производим сдвигание вправо на 1, причем область определения становится равной x∈-2; 4. Без изменений остается область значений y∈-π; π.
Задача преобразования графика обратной тригонометрической функции завершена. Если по условию имеются сложные функции, тогда необходимо прибегнуть к полному исследованию функция.
Всё ещё сложно?
Наши эксперты помогут разобраться
Все услуги
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Сжатие (растяжение) графика к (от) оси ординат.Симметричное отображение графика относительно оси
Первая группа действий связана с умножением АРГУМЕНТА функции на число. Для удобства я разобью правило на несколько пунктов:
Сжатие графика функции к оси ординат
Это случай когда АРГУМЕНТ функции умножен на число, бОльшее единицы.
Правило: чтобы построить график функции , где , нужно график функции сжать к оси в раз.
И первой на эшафот взойдёт функция, которой я недавно грозился:
Пример 1
Построить график функции .
Сначала изобразим график синуса, его период равен :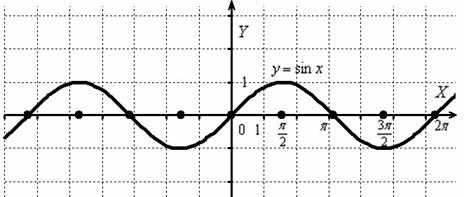
К слову, чертить графики тригонометрических функций вручную – занятие кропотливое, поскольку и т.д., то есть на стандартной клетчатой бумаге аккуратным нужно быть вплоть до миллиметра, даже до полумиллиметра. Впрочем, многие с этим уже столкнулись.
Теперь поиграем на бесконечно длинном баяне. Мысленно возьмём синусоиду в руки и сожмём её к оси в 2 раза: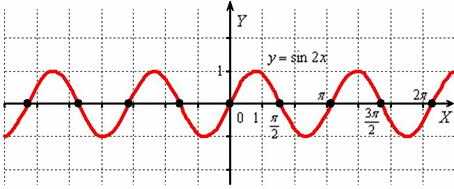
То есть, график функции получается путём сжатия графика к оси ординат в два раза. Логично, что период итоговой функции тоже уполовинился:
В целях самоконтроля можно взять 2-3 значения «икс» и устно либо на черновике выполнить подстановку:
Смотрим на чертёж, и видим, что это действительно так.
Аналогичную блиц-проверку полезно осуществлять в любом другом примере! Более того, она лучше поможет усвоить суть того или иного преобразования.
Пример 2
Построить график функции
«Чёрная гармошка» сжимается к оси в 3 раза: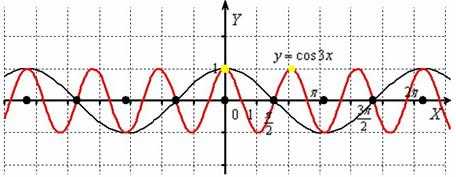
Итоговый график проведён красным цветом.
Исходный период косинуса закономерно уменьшается в три раза: (отграничен жёлтыми точками).
Растяжение графика функции от оси ординат
Это противоположное действие, теперь баян не сжимается, а растягивается.
Случай имеет место, когда АРГУМЕНТ функции умножается на число .
Правило: чтобы построить график функции , где , нужно график функции растянуть от оси в раз.
Продолжим мучить синус:
Пример 3
Построить график функции
Берём в руки нашу «бесконечную гармошку»: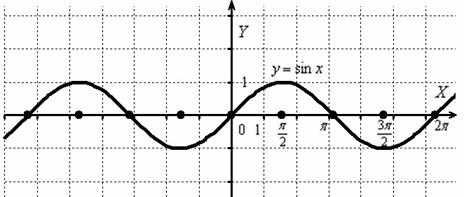
И растягиваем её от оси в 2 раза: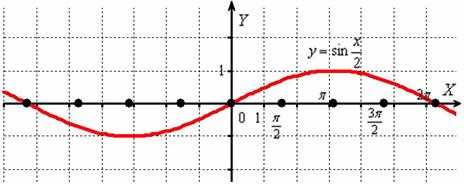
То есть, график функции получается путём растяжения графика от оси ординат в два раза. Период итоговой функции увеличивается в 2 раза: , он толком даже не вместился на данный чертёж.
Операции сжатия/растяжения графиков, разумеется, выполнимы не только для тригонометрических функций:
Пример 4
Построить графики функций
График функции получается путём сжатия графика экспоненты к оси в два раза. А график – путём растяжения графика экспоненты от оси в два раза:
В качестве ассоциации можете опять поиграть на «баяне» .
Продолжаем систематизировать умножение аргумента функции на число:
Мы рассмотрели два случая – сжатие () и растяжение ().
Очевидно, что нет практического смысла рассматривать значения . Есть более интересный вопрос: что происходит, когда аргумент умножается на отрицательное число? Ответ будет получен чуть позже, а пока рассмотрим распространённый частный случай, когда :
Симметричное отображение графика функции относительно оси ординат
АРГУМЕНТ функции меняет знак.
Правило: чтобы построить график функции , нужно график отобразить симметрично относительно оси .
Наглядный пример уже встречался на уроке Графики и свойства элементарных функций (вспоминаем ). Распечатаем ещё один комплект:
Пример 5
Построить график функции
График функции получается путём симметричного отображения графика относительно оси ординат:
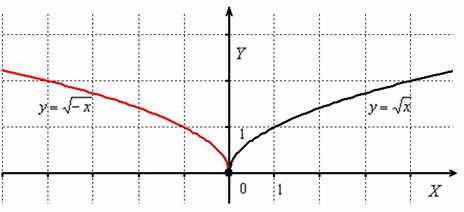
Как видите, всё просто.
Если при умножении аргумента на число значение параметра отрицательно и не равно минус единице, то построение выполняется в два шага. Например: . На первом шаге выполняем сжатие графика к оси ординат в 2 раза: . На втором шаге график отображаем симметрично относительно оси ординат: . Конкретный пример обязательно рассмотрим ниже.
А следующий параграф посвящается одному интересному человеку из дворовой компании моего далёкого детства. Он вытягивал руки в стороны, открывал рот и прыгал влево/вправо по проезжей части. Водители крутили виском у пальца, сигналили, но догнать его так никто и не смог.
Изменение маркеров точек у графиков
Наконец, можно
поменять тип маркеров у точек. Для этого в форматную строку достаточно
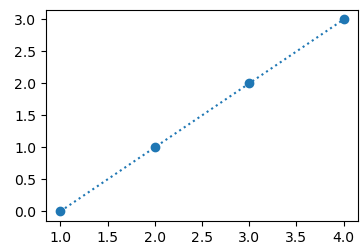
прописать один из предопределенных символов. Например, вот такая запись:
plt.plot(x2, y2, ':o')
отображает
график с круглыми точками:
Какие типы
маркеров еще могут быть? Они перечислены в таблице ниже:
|
Обозначение |
Описание |
|
‘o’ |
|
|
‘v’ |
|
|
‘^’ |
|
|
‘<‘ |
|
|
‘>’ |
|
|
‘2’ |
|
|
‘3’ |
|
|
‘4’ |
|
|
‘s’ |
|
|
‘p’ |
|
|
‘*’ |
|
|
‘h’ |
|
|
‘H’ |
|
|
‘+’ |
|
|
‘x’ |
|
|
‘D’ |
|
|
‘d’ |
|
|
‘|’ |
|
|
‘_’ |
Используются все
эти символы очевидным образом. Причем, записывать их можно в любом порядке с
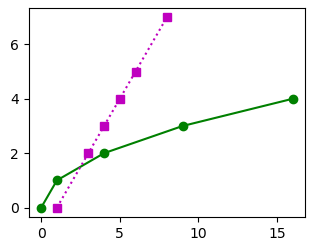
другими форматными символами:
lines = plt.plot(x, y, '-go', x2, y2, 's:m')
отобразится
следующий график:
Другой способ
определения маркера – использование параметра marker:
lines = plt.plot(x, y, '-go', x2, y2, 's:m', marker='d')
В этом случае
для обоих графиков будет присвоен один и тот же маркер типа ‘d’. Для задания
цвета маркера, отличного от цвета линии, применяется параметр markerfacecolor:
lines = plt.plot(x, y, '-go', x2, y2, 's:m', marker='d', markerfacecolor='w')
Здесь мы выбрали
белый цвет заливки и графики теперь выглядят так:
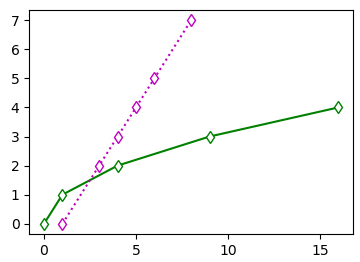
Включаем автопрокрутку и отступ справа
По умолчанию в большинстве торговых терминалов включена функция автопрокрутки. Она работает так. Вы отматываете график «в прошлое», но как только цена хоть чуть-чуть изменится – график автоматически вернется «в настоящее».
Чтобы провести анализ рынка, приходится иногда делать несколько «отмоток» назад. И когда вы вот так отматываете, а вас перекидывает обратно – это жутко раздражает.
Поэтому на время анализа можно отключить автопрокрутку. В Метатрейдере она отключается тут:
Когда она отключена, можно спокойно мотать график в прошлое и при желании возвращаться в настоящее.
Еще одна полезная вещь – смещение графика. Если оно включено, у вас после графика появится немного свободного места.
Это бывает нужно для технического анализа. Например, чтобы построить равноудаленный канал и составить прогноз о целях движения цены.
Если смещения нет – котировки будут утыкаться в правый край графика и техническую аналитику вести будет сложнее:
Собственно, мы сделали все необходимые настройки, теперь давайте читать наши с вами графики.
Линии тренда
Для создания
линии трейда на графике проделайте следующие действия:
1. нажмите и
удерживайте клавишу Shift. Курсор мыши примет форму карандаша, показывая что активизирован режим
создания новой линии тренда;
2. установите
курсор мыши в точку начала линии тренда и нажмите левую кнопку мыши;
3. переведите
курсор в точку окончания линии тренда и отпустите кнопку мыши. Новая линия
тренда отобразится на графике.
4. для отказа от
проведения новой линии отпустите клавишу Shift.
Для просмотра существующих линий тренда
выберите пункт «Линии тренда» из контекстного меню графика. (Данный
пункт меню не активизируется до тех пор пока не будет нарисована хотя бы одна
линия.)
Чтобы выделить
нужную линию на графике выберите одну из строк таблицы. Соответствующий отрезок
на графике отобразится штрих-пунктирной линией.
Для удаления
выбранной линии тренда нажмите кнопку <Удалить>. Вы можете
Чтобы выйти из
диалога нажмите кнопку <Закрыть>.
7 Графики синуса и косинуса
Построим график функции . При этом нам опять пригодятся
часы из разд. 2.1.
Если , то, очевидно, . Когда возрастает от 0 до
, число возрастает от 0 до 1 (представьте себе,
как меняется ордината конца стрелки на наших фирменных часах).
Участок графика для от 0 до изображен на
рис. .
При
Чем ближе к , тем более полого идет наша кривая. Это
происходит потому, что проекция конца стрелки на ось
ординат, колеблясь по отрезку , быстрее всего
движется в середине отрезка и замедляется у его краев: мы
это уже обсуждали в разд. 2.1.
симметричны относительно прямой
Задача 7.1
Запишите уравнение прямой, касающейся графика функции
в точке с координатами .
Кривая на рис б
центрально симметрична относительно точки
с координатами ; это следует из другой формулы
приведения:
(рис. б).
После того, как у нас есть участок графика функции для
, весь график строится уже просто. В самом деле,
когда конец стрелки прошел путь , стрелка вернулась
в исходное положение; при дальнейшем движении все будет
повторяться. Значит, график будет состоять из таких же кусков,
как на рис б. Окончательно график функции
выглядит так, как на рис. .
Теперь построим график функции . Можно было бы строить его так же, как
мы строили график синуса. Мы, однако, изберем другой путь,
который позволит использовать уже имеющуюся у нас информацию.
Именно, воспользуемся формулой приведения
. Эту формулу можно понимать так: функция
принимает те же значения, что и функция , но на
раньше. Например, функция принимает значение 1 при
, а функция
принимает это же
значение уже при . На графике это означает следующее: для
каждой точки графика есть точка графика ,
у которой ордината та же, а абсцисса на меньше
(рис. ).
сдвинуть график
Итак, мы выяснили, что график косинуса получается преобразованием
(сдвигом) из графика синуса. Случаи, когда график одной функции
можно получить преобразованием из графика другой функции,
интересны и сами по себе, поэтому скажем о них несколько слов.
Как, например, будет выглядеть график функции ? Ясно,
что ординаты точек этого графика получаются из ординат
соответствующих точек графика умножением на 2, так что
наш график изобразится сплошной кривой на рис. . Можно
сказать, что график получается из графика растяжением в два раза вдоль оси
ординат.
сжатием в 2 раза к оси ординат.
Попробуем еще построить график функции
.
Понятно, что он должен получаться каким-то преобразованием из
графика . На первый взгляд может показаться, что это
преобразование — сдвиг влево на вдоль оси абсцисс, по
аналогии с тем, что изображено на рис. . Однако, если
бы это было так, то вышло бы, например, что функция
принимает значение 1 при
, что не соответствует действительности
(проверьте!). Правильно рассуждать так:
, так что функция
принимает те
же значения, что и функция , но на раньше. Так
что сдвиг влево — не на
, а на (рис. ).
Кривые, являющиеся графиками функций
, где ,
, называются синусоидами. Заметим, что кривой
«косинусоида» вводить не надо: как мы видели, график косинуса
— это та же кривая, что и график
синуса, только иначе
расположенная относительно осей координат.
Задача 7.2
Каковы координаты точек, помеченных на
рис. вопросительными знаками?
Задача 7.3
Возьмите свечу, тонкий лист бумаги и острый нож. Намотайте лист
бумаги на свечу в несколько слоев и аккуратно разрежьте эту свечу
вместе с бумагой наискосок ножом. Теперь разверните бумагу. Вы
увидите, что она оказалась разрезанной по волнистой линии.
Докажите, что эта волнистая линия является синусоидой.
Задача 7.4
Постройте графики функций:
Замечание. Если вы строите графики
тригонометрических функций на клетчатой бумаге, удобно выбрать
немного разные масштабы по осям, с тем чтобы на оси абсцисс
числу соответствовало целое число клеточек. Например, часто
выбирают такой масштаб: по оси ординат отрезок длины 1 занимает
две клеточки, по оси абсцисс отрезок длины занимает 6
клеточек.
Задача 7.5
Постройте графики функций:
а)
;
б)
.
Посмотрим, как выглядят на графиках уже известные нам решения
уравнений и . Эти решения являются
абсциссами точек пересечения горизонтальной прямой
с графиком функций (соответственно ). На
рис. , хорошо видны две серии решений,
получающихся при .
По графикам синуса и косинуса видно, на каких промежутках эти
функции возрастают, а на каких убывают. Ясно, например, что
функция возрастает на отрезках
,
,
,…- одним словом, на
всех отрезках
, где
,
и убывает на всех отрезках
, где
.
Задача 7.6
На каких отрезках возрастает и на каких убывает
функция ?
Задача 7.7
Сравните числа:
Задача 7.8
Расположите в порядке возрастания:
, , , , , .
Написать комментарий
Выбор стиля графика
Нажимая клавишу , Вы можете
выбрать один из следующих стилей.
Линейный график
Представляет собой последовательность
отрезков, соединяющих точки, отражающие цену последней сделки за каждый период
времени.
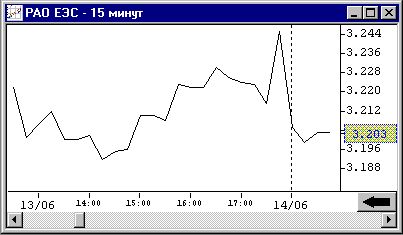
График в виде свечей
Верхняя часть свечи показывает наибольшую,
а нижняя часть –наименьшую цену сделки
за данный период. Цвет свечи сигнализирует о направлении изменения цены.
Закрашенная свеча означает, что цена закрытия ниже цены открытия. Незакрашенная
свеча означает, что цена закрытия периода выше цены открытия.
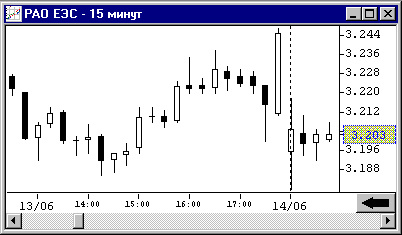
График в виде баров
Верхняя точка каждого бара показывает
максимальное, а нижняя точка – минимальное значение цены за данный период.
Левая отметка указывает цену открытия, а правая – цену закрытия периода.
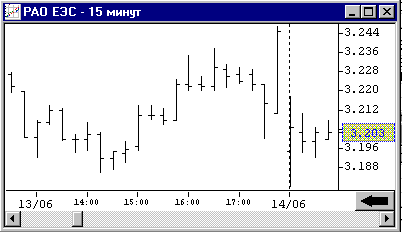
График баров
Это уже более сложный график. График баров показывает цены открытия и закрытия, а также максимальную и минимальную цену.
Самая нижняя точка бара показывает минимальную котировку валютной пары за определенный промежуток времени, верхняя точка показывает максимальную котировку валютной пары за определенный промежуток времени.
Текущий бар показывает текущий торговый диапазон по валютной паре в целом.
Горизонтальный выступ на левой стороне бара означает цену открытия, а горизонтальный выступ на правой стороне бара означает цену закрытия.
Пример графика баров по валютной паре EURUSD:
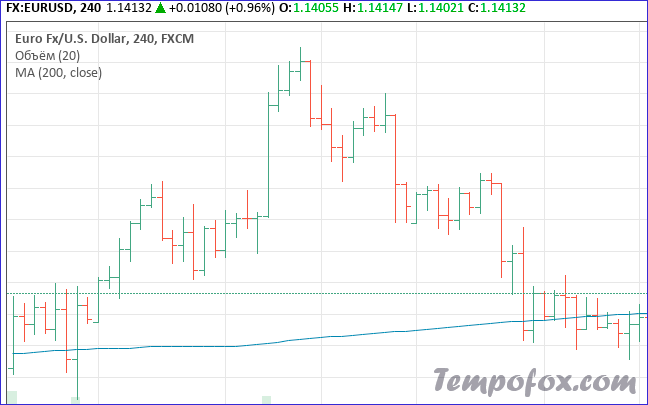
Кстати, некоторые трейдеры часто используют это выражение – «бар». По сути бар в этом понимании – это единственный кусочек данных на графике за единицу времени. То есть, один бар – это данные за минуту, час, 4 часа, день и т.д. Временной интервал может быть разный. Если вы поставите в настройках графика вывод данных за 1 час, то 1 бар будет показывать диапазон движения цены за 1 час.
Пример одного бара с пояснениями
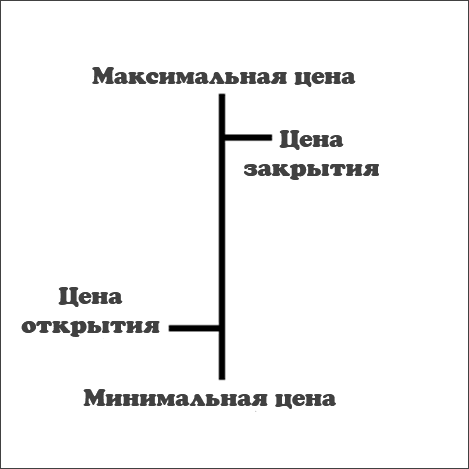
Цена открытия – небольшая горизонтальная полоска с левой стороны бара
Максимальная цена – верхняя точка бара, означает самую высокую цену за выбранный период времени
Минимальная цена – нижняя часть вертикальной линии, означает минимальную цену за выбранный период времени
Цена закрытия – небольшая горизонтальная линия с правой стороны бара. Показывает цену, которая была в момент закрытия периода отображения бара. Если мы ставим период 1 час, то это будет цена, которая была по истечении одного часа.
